Buddy Fishing

Overview and Objectives

This lecture focuses on links between agents. In a Buddy World, links establish collaborative relationships. The Buddy World model is a variation of the Fishing World model.

Goals and Outcomes

This lecture continues to focus on the emergence of systemic regularities from individual-level randomness. Recall that Fishing World established a simplified link between labor and production. While maintaining that link, a buddy world introduces a very basic form of collaboration in production. A core goal of the Buddy World model is to demonstrate that agent collaboration can be a risk-sharing strategy.

This lecture continue to emphasize the acquisition of programming skills that support agent-based modeling and simulation. The focal skill is the ability to create and use persistent links between agents.

Fishing World Prerequisites

Fishing with a Buddy

Goals

This section introduces an apparently small modification of Fishing World. Much of the FishingEconomy01 model is unchanged, but fishers now fish with fishing buddies. Buddies fish together until their joint catch totals two fish. They then split the catch and go home to eat.

The goal in making this change is to compare outcomes in a completely individualistic fisher village to outcomes in a village with economically important social links. There are many possible implementations of this model. The approach described below emphasizes parallels to the Basic Fishing World.

A New Fisher Description

A BuddyFisher resembles a Fisher with a new data attribute (buddy) and a new behavior (share). However, this apparent similarity is partly due to a repurposing of previous behavior names, in order to emphasize parallels with the original fisher type. The behavior of a BuddyFisher is different. Now a fisher can eat only when her buddy can also eat: buddies must have two fish between them in order to eat. The updateFisher activity is correspondingly more complex, as discussed below.

images/umlBuddyFisher.svg — Class Diagram for a BuddyFisher

The buddy attribute creates a new problem for agent initialization: buddies cannot be assigned until fishers are created, but assignment of a buddy is part of the initialization of a fisher. There are various approaches to this problem. For example, when assigning buddies, one could rely on a integer proxy for fishers. That is, associate each fisher with an integer in \([1\,..\,n]\), in anticipation of the creation of \(n\) fishers. With this approach, buddy can be an integer attribute, which locates a fisher by number. Alternative approaches could discard the buddy attribute altogether. For example, introduce a Pair type that creates or links two fishers.

As indicated by the BuddyFisher diagram, this section takes yet another approach. In the diagram, the initial value of buddy is nobody. In this book, this means that the actual assignment of a BuddyFisher to this attribute is postponed (e.g., until after all the fishers are created). How best to accomplish this postponement is language specific.

Create a new project, named FishingEconomy02. This new project will eventually implement the buddy fishing model. You may copy FishingEconomy01 code to FishingEconomy02, as needed. Get started by creating \(1000\) fishers, with attributes and behavior stubs based on figure umlBuddyFisher.

Decentralized Buddy Allocation

The setup phase of a buddy-fisher simulation includes the assignment of a random fishing buddy to each fisher. A variety of approaches can produce this assignment. One of the simplest is for each fisher who lacks a buddy to randomly search for a buddy. (This will not be the approach in this section.) Searching for a buddy might work as follows:

activity:

findBuddy

context:

BuddyFisher

summary:

If this fisher already has a buddy, stop.
If there are any buddyless fishers, choose on of them and buddy up.

The corresponding simulation setup asks each fisher to find a buddy. If there is an odd number of fishers, there will be an odd fisher out. Rather than worry about this, the present section will work with an even number of fishers.

The findBuddy activity depends on a buddyUp activity. This will be a BuddyFisher activity that requires a single input, the intended buddy. The activity must set the attribute of the fisher’s intended buddy as well as the fisher. The following activity summary suggests one approach to implementation.

behavior:

buddyUp

context:

BuddyFisher

parameter:

partner: BuddyFisher

summary:

set buddy to partner, and
set the buddy’s buddy to oneself.

Following the above activity summary, create a buddyUp activity to support the findBuddy activity.

findBuddy

to buddyUp [#partner]
  ask #partner [set buddy myself]
  set buddy #partner
end

Centralized Buddy Allocation

The findBuddy activity implements a decentralized buddy allocation, which is attractive from an agent-based modeling perspective. A decentralized approach highlights the individual actions that produce buddy assignment. One potential drawback, however, is the computational cost. Decentralized buddy finding is a computationally expensive approach to pairing up agents. In other models that need repeated pairing up, the gains to a centralized approach can be large. In the present model, however, this cost matters little: it occurs only once per simulation (during setup), which limits this cost.

Nevertheless, this section explores an alternative, centralized approach to buddy allocation. The primary reason for doing this is to emphasize that code can implement an agent-based conceptual model even when using such a centralized allocation mechanisms. The conceptual model uses a random assignment of buddies, and in this case, the centralized result is equivalent to one achieved in a decentralized manner.

Allowing the computational model to diverge from the most literal implementation of the conceptual model sometimes permits implementation choices based on computational convenience or efficiency. In the present model, with either approach, the final result is a random pairing of the agents in our model. (In fact, in the present model, even the randomness of the pairings is immaterial to the model outcomes.)

Centralized Buddy Allocation: Implementation Details

There are many ways to form pairs of buddies after fisher creation. The best way to pair up the fishers will vary by language. Here is one way that is often feasible. Iterate over all the fishers in random order, buddying up each pair encountered during the iteration. This can be easier if we use a local variable to represent the next buddy can be useful.

Create an assignBuddies activity that buddies up all of the fishers. Create a setup activity that executes the assignBuddies activity.

assignBuddies

to assignBuddies
  let _partner nobody
  ask patches [
    ifelse (nobody = _partner) [
      set _partner self
    ][
      buddyUp _partner
      set _partner nobody
    ]
  ]
end

Partitioning a List

Recall how to buddy up a pair of fisher with the buddyUp activity. With this is mind, one obvious strategy for buddying up a collection of fishers pairs them up first and then buddies up each pair. Beginning with a list of all the fishers, use a partition utility to partition this list into pairs. Then each pair can become buddies.

Some languages provide built-in support for list partitioning; others do not. In most languages, it is fairly simple to write such a function. Here is function summary for one possible approach. Given a list of any type of object and an integer partition size, it returns a list of list of length n. (For simplicity, the inner lists are represented by a List[Any] type.) For example, the partition command can partition a list of fishers into a list of pairs of fishers.

function:

partition: (List[Any], Integer) -> List[List[Any]]

parameters:

xs, a list of any type of objects
n, the length of the non-overlapping sublists

summary:

Return a list of sequential, non-overlapping sublists of xs, where each sublist has length n. (Discard left over items.)

Add a partition function to the FishingEconomy02 project. The partition function should require two inputs (a list and an integer) and produce one output (a list of sublists of the first argument). Use it to create pairs of fishers, and then buddy up each pair.

Hint

Here one way to write a partition function. Note the use of the sublist primitive.

Partitioning a List

to-report partition [
  #xs  ;Any[], the list to partition
  #n   ;Integer, the length of each nested list
  ] ;-> list of sublists
  ;NOTE: all sublists have length #n (remaining items discarded)
  if (#n < 1 or #n != int #n) [error "#n must be a postive integer"]
  let _nparts int (length #xs / #n)
  report n-values _nparts [[?] -> sublist #xs (? * #n) ((? + 1) * #n)]
end

For this exercise, just use this function as is, applying it to a list (not an agentset) of fishers. For example, the following uses will partition the list into pairs and then into triples.

partition [1 2 3 4 5 6] 2  ;partition into pairs
; result is [[1 2] [3 4] [5 6]]
partition [1 2 3 4 5 6] 3  ;partition into triples
; result is [[1 2 3] [4 5 6]]

Centralized Pairing Up of the Fishers

It is possible to write a new assignBuddies activity that depends on the new partition function. The following activity summary suggests one way to accomplish this. First produce the list of pairs. Then, iterate over the all of the pairs, and then buddy up the fishers in each pair. That is, for each pair, set the buddy of each of the two fishers to the other fisher.

activity:

assignBuddies

context:

global

summary:

Produce a list of pairs of fishers using the partition utlity.
For each pair of fishers, use buddyUp to set each fisher as the buddy of the other.

Since we are pairing our fishers, there is always the possibility of an odd man out. For now, avoid that consideration by using an even number of fishers: continue to use 1000 fishers.

Implement the assignBuddies activity, as described above.

assignBuddies

to assignBuddies02
  let _pairs partition ([self] of patches) 2
  foreach _pairs [?pair ->
    ask (first ?pair) [buddyUp (last ?pair)]
  ]
end

Updating a `BuddyFisher`

Once fishers are buddied up, they can fish, share, and eat. Buddy fishing substantially changes the updating of a fisher. Now, a fisher cannot decide alone whether to eat, since she will not eat alone. We will summarize this sequence of behaviors in a new updateFisher activity, as described by the following activity summary.

activity:

updateFisher

context:

BuddyFisher

summary:

If hungry, fish.
If have two fish, share.
If able to, eat and ask buddy to eat.

The activity summary for updateFisher depends on a share activity. A fisher with two fish shares one with her buddy, as described by the following activity summary.

activity:

share

context:

BuddyFisher

summary:

Decrement nFish.
Ask buddy to increment nFish.

Add a share activity to this project. Create an updateFisher activity that depends on share, as described above.

updateFisher

to share  ;patch proc
  if not (0 = [nFish] of buddy) [error "accounting error"]
  set nFish (nFish - 1)
  ask buddy [
    set nFish (nFish + 1)
  ]
end

to updateFisher [#p]
  if (0 < nEaten) [stop]
  fish #p
  if (nobody != buddy and 2 = nFish) [share]
  if (canEat) [
    eat
    if (nobody != buddy) [ask buddy [eat]]
  ]
end

Simulation Schedule for `FishingEconomy02`

The simulation schedule for FishingEconomy02 closely resembles the schedule for FishingEconomy01. Recall that the probability that a fisher’s cast actually catches a fish is a model parameter. The core of the schedule is that each hungry fisher fishes and then decides with a buddy whether to eat. The updateFisher activity embodies these core considerations, as described above.

Create a step activity that updates all the fishers. In addition, it should increment the tick counter, in order to keep track of the number of steps.

updateFisher

to step
  ask patches [updateFisher p] ;update fishers
  tick
end

Simulating a Village’s Day (Buddy Fishing)

By watching the evolution of the village during a day, it is easier to keep track of how the number hungry fishers changes as the day wears on.

Simulate a day of fishing in FishingEconomy02 by repeatedly executing the simulation schedule. Once again, tally the number of fishers who are still hungry as the day progresses. Add GUI support as in the FishingEconomy01 project.

Chart an empirical survival function for the hungry in this buddy0fishing economy. Compare this result to our previous (Fishing Alone) economy. If you detect differences, try to explain them. (Add explanatory comments in your program file.)

Export the survival data, and read your data into a spreadsheet. Create an empirical survival plot, which you should save as buddySurvival.png.

A Typical Day (Buddy Fishing)

It is still the case that some fishers stop fishing early in the day, while others must continue fishing. And once again, only the hungry continue to fish. As an illustration, an economy with only \(100\) fishers and a 0.01 chance of success each cast, which may produce a result like the following.

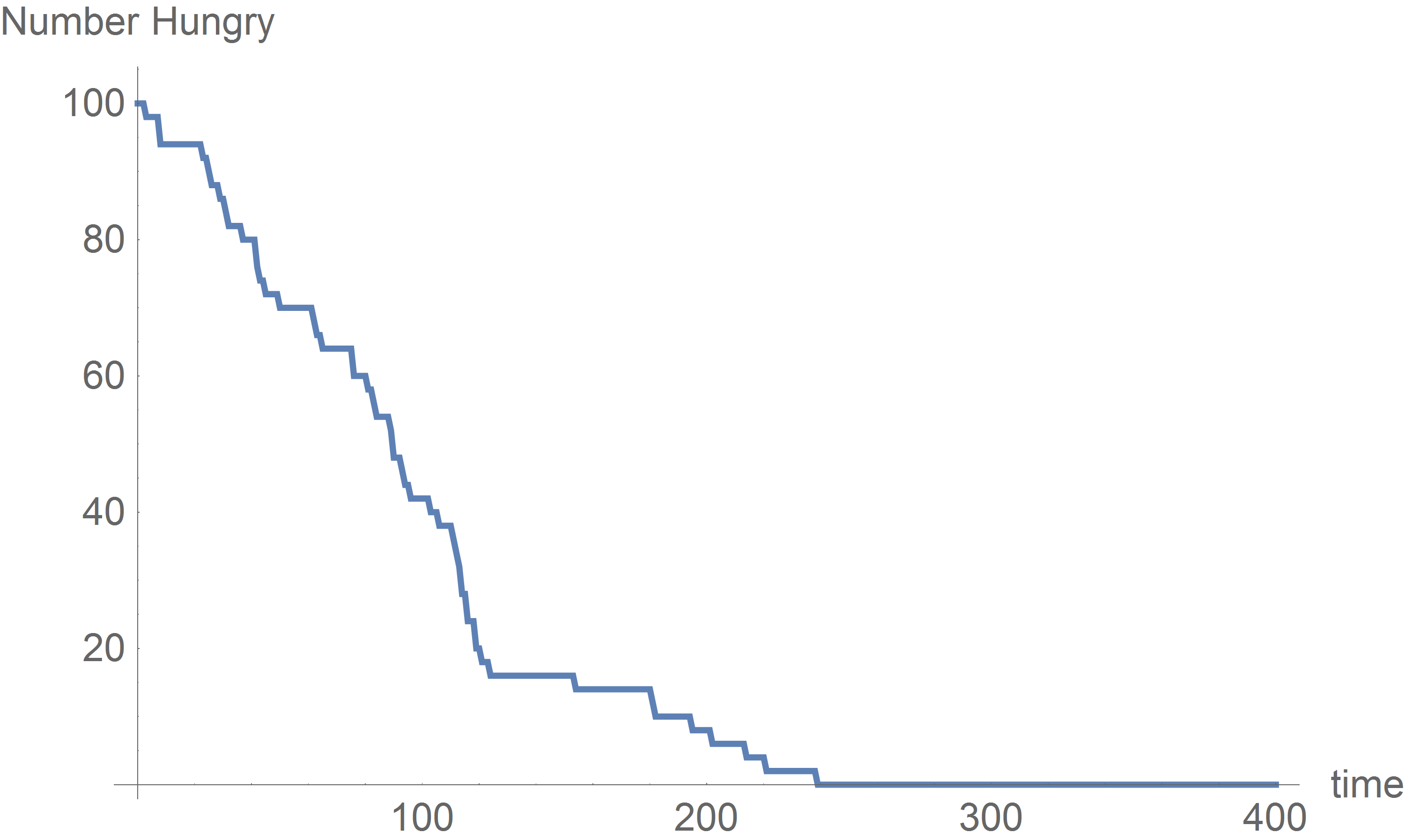
images/hungry-history03.png — One Village Day: `nFishers=100`, `p=0.01`

It appears that in a village of buddy fishing, it is less likely that anyone will go hungry at the end of the day. However, this does not mean that the villagers perform less work altogether. On average, it still takes the same number of casts to feed everyone.

Exploration, Resources, and References

Buddy World Explorations

Change the assignBuddies activity to require an input: the agents to be buddied up.
Explain in detail how to partition two lists into two equal-length sublists. Create a partition utility and a test for it.
In the buddy-fishing model, change canEat to handle the case of an odd number of fishers. A lone fisher (i.e., one with no buddy) can eat if she has a fish.
Since the FishingEconomy01 and FishingEconomy02 projects use the same step activity, try to move it into a shared module.

NetLogo-Specific Explorations

Since the FishingEconomy01 and FishingEconomy02 projects use the same step activity, try to move it into a shared module.
Since the FishingEconomy01 and FishingEconomy02 projects use the same step activity, try to move it into a shared module.
Since the FishingEconomy01 and FishingEconomy02 projects use the same step activity, try to move it into a shared module.

References

[Downey-2015-GreenTeaPress]

Downey, Allen B. (2015) Think Python: How to Think Like a Computer Scientist. Needham, MA: Green Tea Press. https://greenteapress.com/wp/think-python-2e/

version:: 2024-05-15

Buddy Fishing

Overview and Objectives

Goals and Outcomes

Fishing World Prerequisites

Fishing with a Buddy

Goals

A New Fisher Description

Decentralized Buddy Allocation

Centralized Buddy Allocation

Centralized Buddy Allocation: Implementation Details

Partitioning a List

Centralized Pairing Up of the Fishers

Updating a BuddyFisher

Simulation Schedule for FishingEconomy02

Simulating a Village’s Day (Buddy Fishing)

A Typical Day (Buddy Fishing)

Exploration, Resources, and References

Buddy World Explorations

NetLogo-Specific Explorations

References

Updating a `BuddyFisher`

Simulation Schedule for `FishingEconomy02`