Sugarscape
Overview and Objectives
This lecture develops a simple version of the famous Sugarscape model of [Epstein.Axtell-1996-MIT]. In this model, a population of mobile agents compete for a renewable resource that is spatially dispersed. [Kendrick.Mercado.Amman-2006-PrincetonUP] suggest thinking of the terrain as comprising the possible locations for small businesses, where business profitability is location dependent. Under this interpretation, an agent chooses a location for the production of profits, where the of profit potential varies by location. To spice things up, agents continually seek more profitable locations, but only one agent at a time can occupy any particular location. In addition, agents have resource needs, and if an agent cannot meet its needs it will go bankrupt and exit the terrain.
A core goal of this lecture is to introduce a very early model of emergence where agents interact with a spatial environment. The Sugarscape model is an early agent-based model that has become a paradigm of the “generative approach” to social science [Epstein-1999-Complexity]. Mobile autonomous agents compete for resources, and outcomes such as average survival rate, the distribution of wealth, and patterns of movement across the terrain emerge in the process. These outcomes are generated, not imposed, and in these sense they are emergent properties of the entire system.
Goals and Outcomes
This lecture adds spatial considerations to the agent-based modeling and simulation tools introduced in past chapters. It extends the exploration of ways in which substantial heterogeneity can emerge among initially identical agents. Central to the present lecture is the complete development of a simple agent-based model of the emergence of inequality in a world with a constant ability to generate wealth but dispersed opportunities to do so.
Prerequisites
Implementing this lecture’s model requires the mastery of the material in the Financial Accumulation lecture, particularly the exercises therein. While understanding the core concepts in the present lecture does not require attempting the accompanying exercises, these exercises promote a deeper understanding of the model and its consequences. Addtionally, the exercises of this lecture refine programming skills needed for models in future lectures.
Model Basics
Terrain and Resources: Conceptual Model
The Sugarscape model has a spatial dimension, embodied in a two-dimensional terrain. This lecture focuses on the simplest version of the model, which includes a single renewable resource. Traditionally, we call the resource sugar, and we call the terrain and its initial resource distribution the sugarscape. The sugar resource is unequally distributed across the terrain. It is not simply random but instead has areas of concentration and dearth.
Patches
As a computational convenience,
divide the terrain into patches (also called cells).
The typical impelementation of a terrain comprises
a two-dimensional rectangular array of patches.
Patches are non-overlapping square subregions of the terrain.
The array of patches has fixed dimenions,
which is the terrain’s gridsize.
At each array location is a single patch.
The associated array indexes may be considered to be the immutable coordinates of the patch.
For illustration,
Figure sugarscapeEmptyTerrain displays a square terrain
partitioned into equal-sized patches.

Partitioning a Terrain into a Grid of Patches.
Basic Terrain:
The canonical Sugarscape terrain is a \(50 \times 50\) grid of patches.
Begin a new project called Sugarscape01,
and implement the creation of such a terrain.
The Sugar Resource
Patches are associated with the renewable resource in the following ways.
A patch has an immutable sugarMax attribute,
which holds its sugar capacity.
Sugar capacity differs between patches;
they are fundamentally heterogeneous.
In addition, a patch has a mutable sugar attribute,
which holds its actual amount of sugar.
This may differ from its capacity and from the sugar of other patches.
This is another source of heterogeneity among patches.
Canonical Terrain
In the Sugarscape model,
the sugar capacity (sugarMax) of each patch
lies in a specified integer interval.
However, it is not randomly assigned.
In the canonical Sugarscape terrain,
sugar capacity is clustered.
[Epstein.Axtell-1996-MIT] describe this terrain verbally rather than algorithmically.
There are two peaks (with sugar capacity 4), separated by a valley of scarce sugar,
and then surrounded by a desert of sugarless patches.
An image accompanies this description,
and various replication efforts have attempted to extract data from this image.
Terrain Initialization in Sugarscape
An initialized terrain comprises an initialized array of patches.
Intialization of a patch sets the value of its
sugarMax and sugar attributes.
Initially, each patch is at full capacity.
To initialize a patch,
set its sugarMax and sugar attributes
to the same corresponding value in this file.
The following procedure sketch summarizes this process.
- procedure name:
initPatch- context:
Patch- parameter:
s, the sugar capacity- summary:
Set
sugarMaxtos. Setsugartos.
In order to produce a terrain similar to the original,
this lecture takes the resource capacity (sugarMax)
for each patch from the sugar-map.txt file
provided in the NetLogo Models Library. [1]
The data in this file are integer values,
arranged in the same \(50 \times 50\) layout as the terrain.
Each value of the sugar data lies in the integer interval \([0\,..\,4]\).
Correspondingly, for any patch,
the initial values of sugarMax and sugar lie in this interval.
Initial Sugarscape Terrain:
Based on the initPatch procedure sketch,
implement a patch initialization procedure.
(Alternatively, implement a function that consumes a sugar level returns an initialized patch.)
Then copy the sugar-map.txt file from the NetLogo Models Library
into your Sugarscape01 project folder,
and use this file to initialize the terrain in your Sugarscape01 model.
Hint
Implement initPatch as a patch procedure.
Note that sort patches produces a list of all
the terrain’s patches, in row-major order.
Use for-each to iterate over a list.
Use file-open to open the data file for reading.
Each call to the file-read command will successively
read in from the file one number,
which can be used to initialize a patch.
Initial Sugarscape Terrain
to initPatch [#sugar] set psugarMax #sugar set psugar #sugar end
to initTerrain
;; sequentially read Li and Wilensky's sugar-map.txt file,
;; which is based on Figure 1 of Epstein and Axtell
file-open "sugar-map.txt"
foreach sort patches [ ?patch ->
ask ?patch [initPatch file-read]
]
file-close
end
Hint
For this project,
let a patch be an association with two keys:
"sugar" and "sugarMax".
Create an initPatch function that consumes one input (s)
and returns an initialized patch.
Import the sugar-map.txt data with the Import command,
using the "Table" format.
This creates a matrix of sugar capacities.
To create the initial terrain,
map the initPatch function over this matrix
(using a level specification for Map).
Initial Sugarscape Terrain
For example, after setting pth to the filepath for the sugar data:
ss`sugarss = Import[pth, "Table"];
ss`initPatch = s |-> <|"sugar" -> s, "sugarMax" -> s|>;
ss`initTerrain[mS_] := Map[ss`initPatch, mS, {2}]
terrain = ss`initTerrain[sugarmapNML]
Visualization of the Canonical Terrain
One way to visualize the data in the sugar-map.txt file
is to examine it with a text editor.
A better way is to create an image based on this data.
The traditional visualization assigns a color to each patch,
based on its capacity (sugarMax).
In the canonical Sugarscape model,
the capacity of each patch—its sugarMax—lies
in the integer interval \([0\,..\,4]\).
[Epstein.Axtell-1996-MIT] use tints of yellow,
varying from white (no sugar capacity) to very yellow (capacity of 4).
Figure sugarmap takes the same approach,
but on a gray instead of a yellow scale.
Since a darker gray indicates greater sugar capacity,
it is clear that there are two areas of greater resource concentration.

Visualization of the Sugarscape Terrain
Sugar levels in \(\{0, 1, 2, 3, 4\}\). White = 0; darker gray = more sugar.
Patch Behavior
In the basic Sugarscape model, there is one patch behavior: regenerating the renewable resource whenver it is below capacity. This behavior is captured by a single growback rule that governs the entire terrain. [Epstein.Axtell-1996-MIT] summarize the growback rule with the following function, which consumes the resource level (\(s\)) and capacity (\(s_\max\)) of a patch and returns the updated resource level of the patch.
The parameter \(s_\max\) receives the patch-specific carrying capacity (sugarMax),
which is a nonnegative integer.
The parameter \(s\) receives the current resource level of the patch (sugar),
which is a nonnegative integer.
So a patch can regrow sugar at a terrain-specific rate,
but only up to its maximum capacity.
The growback function is parametrized by the growback rate (\(\alpha\)),
which is a positive integer.
This is the maximum amount of sugar that any patch might be able to grow back in one period.
In contrast to the other parameters,
\(\alpha\) is a model parameter that applies to the entire terrain.
The following function sketch summarizes these considerations.
- function:
nextSugar: (Integer,Integer,Integer) -> Integer- parameters:
\(\alpha\), the growback rate
\(s_\max\), a patch’s capacity (maximum sugar level)
\(s\), a patch’s current sugar level
- summary:
Return the minimum of \(s + \alpha\) and \(s_\max\).
Growback Rule:
Implement and test the nextSugar function.
Note
When \(s=s_\max\), the function output has the same value. When \(0=s_\max\), the function output is zero.
Growback Rule
to-report nextSugar [ #alpha ; EA’s alpha, the growback rate #smax ; the maximum sugar capacity of the patch #s ; the current sugar level ] let _next (#s + #alpha) report min (list _next #smax) end
Immediate Growback
The simplest Sugarscape model uses an immediate-growback rule,
where renewal always completely restores any patch to its full capacity.
With immediate growback, it takes only a single renewal cycle for a patch
to reset its value of sugar to its value of sugarMax.
[Epstein.Axtell-1996-MIT] characterize the immediate growback rule as \(G_\infty\),
since any patch fully generates its resource.
On the original terrain, the maximum sugar capacity is \(4\),
in which case the rule \(G_4\) produces immediate growback.
Immediate Growback:
Add a model parameter named sugarGrowRate
to your Sugarscape01 model.
This parameter plays the role of \alpha in [Epstein.Axtell-1996-MIT].
Implement and test a growback procedure,
which uses the nextSugar function to reset the sugar level at a location,
making use of the new sugarGrowRate parameter.
Hint
Add the sugarGrowRate parameter as a slider in your model’s Interface tab.
To ensure immediate growback (with the default terrain),
use a startup procedure to set the default value of \(4\).
Let growback be a patch procedure.
Immediate Growback
to growback ; patch procedure;; regenerate the patch's sugar set psugar (nextSugar sugarGrowRate psugarMax psugar) end
Terrain Summary
So for, the world of the Sugarscape model is very simple.
This world has a sugarGrowRate attribute (EA’s \(\alpha\)),
which governs renewal of the single resouce (“sugar”).
This world has a terrain,
which comprises a fixed set of \(2500\) patches in a \(50 \times 50\) grid.
Each patch has a maximum sugar capacity (sugarMax),
which is immutable.
Each patch also has a current resource level (sugar),
which is mutable.
There is a single patch behavior (growback),
which renews a patch’s resource whenever it is below the patch’s capacity.
Patches are immobile. (A patch’s location on the grid may be considered an immutable patch attribute.) The next step in the development of the Sugarscape model is to add mobile agents. These agents move about the terrain and consume the renewable resource.
Agents
Agent Attributes
Agents are heterogeneous: they differ in metabolism, vision, and wealth. An agent’s metabolism is how much sugar the agent must consume each period in order to stay alive. An agent’s vision determines the sensing distance of the agent (as described below). An agent’s metabolism and vision never change. However, an agent can change its wealth. Agents can also move to different locations on the terrain.
- immutable attributes
visionmetabolism
- mutable attributes
\(w_1\) (the agent’s accumulated sugar wealth)
location
Agent Initialization
Following [Epstein.Axtell-1996-MIT] the canonical Sugarscape initialization randomly chooses an agent’s metabolism from the integer interval \([1\,..\,4]\) and vision from the integer interval \([1\,..\,6]\) For an agent’s initial sugar wealth, [Epstein.Axtell-1996-MIT] randomly choose values from the integer interval \([5\,..\,25]\). However, approaches in the literature vary. For example, [Kendrick.Mercado.Amman-2006-PrincetonUP] set each agent’s sugar endowment to the sugar available at the agent’s initial location. These choices have little effect on the model outcomes. Therefore this lecture more simply gives every agent an inital sugar endowment of \(15\). (This is the mean endowment in the original Sugarscape model.)
Agents Compete for Spatial Locations
Each agent has a location on the terrain. Capture the idea that agents compete for spatial locations with a solo-occupancy constraint: an agent is always located on a patch, and a single patch always has at most one agent. Initialization of an occupied terrain therefore requires associating each agent with a patch. The initial allocation of agents to patches will be entirely random. For simplicity, an agent’s location is the coordinates of its patch.
Populating the Terrain
The initial [Epstein.Axtell-1996-MIT] Sugarscape model has \(400\) agents and \(2500\) patches, which is a population density of \(0.16\). Turning this around, given a target population density of \(0.16\) and a terrain of \(2500\) patches, the Sugarscape model requires \(400\) agents.
The solo-occupancy constraint means that agent locations cannot be determined independently. Two alternatives immediately present themselves. First, one might randomly select as many patches as there are agents, and then populate each patch with an agent. Alternatively, one might sequentially attempt a random placement of each agent, trying again whenever an agent finds its assigned patch is already occupied. We will implement the first of these alternatives.
Initial Agents:
Introduce a popDensity model parameter,
with a default value of \(0.16\).
Compute the number of agents to create based on the target population density
(popDensity) and the number of patches.
Create and initialize the agents.
The agents should be randomly located
but must honor the solo-occupancy constraint:
no two agents should share a location.
Hint
Add a popDensity slider in the Interface tab
of your Sugarscape01 model.
Use NetLogo’s n-of reporter to randomly choose the patches
for the initial agents.
Each chosen patch can sprout an agent.
NetLogo turtles always know their location.
When initializing metabolism and vision,
use the randomInteger function developed in the lecture on zero-intelligence traders.
Initial Agents
to initAgent ;; agt procedure set metabolism (randomInteger 1 metabolismMax) ;; EA p.24 set vision (randomInteger 1 visionMax) ;; EA p.24 ;; to reduce initial variation, use mean of EA's random endowments: set w1 15 ;; or, uncomment next line to use EA endowments: ;set w1 (randomInteger 5 25) ;; EA p.33 end
to setupAgents let _n round (popDensity * count patches) ask n-of _n patches [sprout-agts 1 [ initAgent ]] ;; create & initialize agts end
Visualize Inhabited Terrain
To visualize the inhabited terrain, mark each location that has an agent on top the terrain visualization. Figure inhabitedSugarscape represents agents as a white circle with a black border. The initial location of each agent is random, so there is no discernible pattern to the agent locations.

Visualization of Initial Terrain and Agents
Circles indicate the initial agent locations.
Agents as Gatherers
Mobile agents interact with their environment.
In the basic Sugarscape model,
the core economic activity of an agent is to gather sugar.
The gather activity is particularly simple:
the agent extracts all of the renewable resource (sugar)
at its current location.
The consume activity reduces the agent’s wealth
by the value of its metabolism.
Since the agent continually consumes the renewable resource in order to live,
gathering adequate sugar is the key to logevity.
The following agent-behavior sketches summarize
the concepts underpinning the two activities.
- behavior:
gather- context:
Agt- summary:
Extract all sugar from the current patch and add it to current wealth.
- behavior:
consume- context:
Agt- summary:
Subtract
metabolismfrom current wealth. If wealth thereby falls below zero, the agent dies.
Gather and Consume:
Implement the gather and consume behaviors for the agents.
Hint
While gathering and consumption are separate behaviors in the conceptual model, it may be more efficient to combine them in the computational model. Note that gathering produces complete extraction, so the patch temporarily becomes devoid of sugar.
Gather and Consume
Gathered sugar adds to wealth (w1) but consumption reduces it.
to gatherConsumeDie ;; agt procedure let _sugar psugar set psugar 0 set w1 (w1 + _sugar - metabolism) if (w1 <= 0) [die] end
Agent Sensing
Agents have a bounded ability to sense their local environment.
The vision attribute embodies this limitation:
it determines how much of its immediate environment an agent can perceive.
The perceived environment is the agent’s neighbourhood.
The original Sugarscape model uses a cross neighborhood,
and the value of this attribute is the radius of the neighborhood.
That is, an agent’s vision is the distance that the agent
can perceive in each of the four main directions:
north, south, east, and west.
Figure f:crossHood illustrates a cross neighborhood of radius \(3\) for one agent.
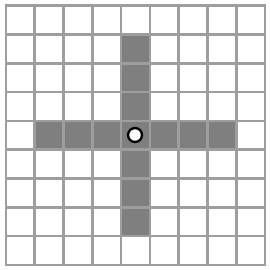
Cross Neighborhood
Squares indicate patches. A circle indicates an agent location. Gray patches are the cross neighborhood of radius \(3\) for this agent.
The locations of the neighborhood patches may be described in terms
of their \(\langle dx,dy \rangle\) offsets from the center patch.
For example, given a radius of \(1\),
the offsets would be
\(\{
\langle 0, 0 \rangle,
\langle 1, 0 \rangle,
\langle 0, 1 \rangle,
\langle -1, 0 \rangle,
\langle 0, -1 \rangle \}\).
Since the collection offsets depend only on the radius,
it should be possible to create a crossOffsets function
to produce the entire collection.
The following function sketch states that the function
should return a collection, such as a list or set.
The members of this collection will be the offsets,
as \(\langle dx,dy \rangle\) pairs.
Be a little careful about handling the central point,
which has offsets \(\langle 0, 0 \rangle\).
This should occur only once in the collection.
- function:
crossOffsets: Integer -> Collection- parameter:
\(r\), the radius (\(r \ge 0\))
- summary:
Return a collection of all of the \(\langle dx,dy \rangle\) offsets for a cross neighborhood of radius \(r\).
Cross Offsets:
Create a crossOffsets function that, given a radius,
produces a representation of a cross neighborhood
as a collection of \(\langle dx,dy \rangle\) offsets.
Hint
Return a list of lists, where each inner list is a [dx dy] pair.
Note that given the value of v,
evaluating the expression (range 1 (1 + v)) produces a list
of the numbers in the integer interval \([1\,..\,v]\),
and evaluating the expression (range (- v) (1 + v)) produces a list
of the numbers in the integer interval \([-v\,..\,v]\).
Cross Offsets
There are many good approaches to this exercise. This one illustrates the use of a local reporter task to produce the offsets at each distance.
to-report crossOffsets [#r] let _rs (range 1 (#r + 1)) let _f [r -> (list (list (- r) 0) (list r 0) (list 0 (- r)) (list 0 r))] report fput [0 0] (reduce sentence map _f _rs) end
Runtime Precomputation
In the Sugarscape model,
every agent needs to examine its neighborhood every period.
Even though the crossOffsets function is not very computationally costly,
it would still be nice to avoid needlessly recomputing the same value.
In such circumstances,
precomputation can be a useful alternative to repeated computation.
There are various approaches to precomputation.
This lecture consider in-memory runtime precomputation,
where the needed values are computed as part of the model setup
and then kept in memory to be used as needed.
The possible inputs to the crossOffsets are just
the values of the vision attribute of agents,
which constitutes a very small set.
In this case, precomputation is sensible.
Precomputed Offsets:
Add a precomputation of the cross offsets
to the setup phase your your Sugarscape01 model.
Hint
This best way to store your precomputed values depends on
your programming language or simulation toolkit.
Even in a single language,
there are multiple reasonable ways to store your computed values.
For example, since the possible values of vision lie in an
integer interval,
you could store them in a list and access them by index.
Or, if an associative array is available,
you could associate vision values to lists of offsets.
Hint
Use the table extension,
and map each value of vision to a list of offsets.
Use a global variable to store this table.
Precomputed Offsets
to setupGlobals set vision2hood table:make ;; a new table let _visions (range 1 (visionMax + 1)) ;; the possible visions ;; map each vision to its cross neighborhood (as offsets): foreach _visions [?v -> table:put vision2hood ?v (crossOffsets ?v)] end
Crossing Borders
In the center of the terrain, the meaning of a cross neighborhood is clear. However, additional specifics are needed at the terrain edges. There are two popular approaches: discard the offsets that would extend beyond the edges, or wrap them to the opposite edges. In the second approach, the terrain effectively becomes a projection of a torus. The original Sugarscape model uses a torus topology, so this lecture does so as well.
Given any location in the Sugarscape grid,
learn how to turn the cross neighborhood represented by crossOffsets
into locations on the grid.
Recall that this grid is a torus, so be sure to wrap at the boundaries.
Hint
In the Interface table,
under the Settings button,
choose to wrap the world horizontally and vertically.
(Or, use the __change-topology primitive to do this.)
After that, the results of the at-points reporter
will automatically wrap when needed.
Preferences
Agents have preferences. A patch with more sugar is always preferred. After that, a patch that is closer is always preferred. (When preference rank multiple criteria in this fashion, they are lexicographic.) Nevertheless, ties are possible: two patches are equally attractive if they have the same amount of sugar and are the same distance away.
However, agents have a limited ability to sense their surrounding environment. Each agent can sense only a cross neighborhood, with radius equal to the agent’s vision. The collection of the most attractive patches in this neighborhood is the agent’s set of local maximizers. These are the most preferred patches among those the agent can perceive.
- function:
maximizers: (location,radius) -> Collection- parameter:
location, the location of the agentradius, the cross-neighborhood radius (\(r \ge 0\))
- summary:
Return a collection of all of the maximizing locations for a cross neighborhood of radius \(r\) centered at
location.
Hint
Each location in the collection may be represented by its coordinates. Alternatively, when a patch knows its coordinates, Each location in the collection may be represented by its patch.
Local Maximizers:
Hint
In order to convert a coordinate that falls outside of the terrain into one that falls within the terrain, use modular arithmetic.
Agent Behavior
Agents are autonomous in the following sense: an agent’s behavior responds to that agent’s attributes and environment. Agents explore the sugarscape by looking nearby for patches that are rich in sugar. An agent is optimizing: it moves to the best available patch it can see. A patch is available whenever no other agent occupies it. Among the available patches, a patch with more sugar is better than a patch with less, and a patch nearby is better than one further away. This ranking is lexicographic: an agent will always move further to get more sugar.
Each agent needs sugar to survive, but an agents also has the capacity to accumulate sugar wealth (\(w_1\)).
An agent's sugar wealth is incremented at the end of each time-step by the sugar collected and decremented by the agent's metabolic rate. However this movement is constrained by its neighbors: no two agents share a location. Two agents are not allowed to occupy the same patch in the grid.
Simulation Schedule
At each tick, each agent will
move to the nearest unoccupied location within their vision range with the most sugar (their own patch is a candidate when moving)
collect all the available sugar there. If its current location has as much or more sugar than any unoccupied location it can see, it will stay put.
use (and thus lose) a certain amount (metabolism) of sugar each tick.
if an agent runs out of sugar, it dies and (in the first model) is simply removed from the simulation
Movement (Environment Topology)
There is at most one agent at each location of the terrain.
torus topology: location coordinates wrap around the edges
Model 1: Distinguishing Features
Model 1: Setup
400 agents, each placed on random unoccupied patch (no dual occupancy)
each agent can only see a certain distance (vision, in [1,6]) horizontally and vertically
each agent has a certain sugar need (metabolism, in [1,4])
Setup
- agents
age 0
randomly chosen unoccupied initial location,
random attributes (vision, metabolism, max-age, initial wealth w0)
random attribute values are drawn from uniform distributions with ranges specified below
Model Rules
- patch growback rule Gα:
each patch grows α units of sugar per time-step, up to the patch's capacity
- agent movement rule M:
move to nearest best unoccupied, visible patch (resolving ties randomly)
best = most sugar visible = with vision patches to the N, E, S, W (vNM neighborhood)
collect all sugar at new location, decrement sugar wealth by metabolism
if sugar wealth <= 0, die
- agent replacement rule R:
if an agent dies, it is replaced by a new agent
new agents get the same initializations as initial agents
Scheduling of events
Scheduling is determined by the order in which the different rules G, M and R are fired in the model. Environmental rule G comes first, followed by agent rule M (which is executed by all agents in random order) and finally agent rule R is executed (again, by all agents in random order).
Parameterisation
Epstein & Axtell (1996, pg. 33)
- Growth rate α
1
- Number of agents N
250
- Agents' initial wealth w0
distribution U[5,25]
- Agents' metabolic rate m distribution
U[1,4]
- Agents' vision v distribution
U[1,6]
- Agents' maximum age max-age
distribution U[60,100]
Later Models
Agents:
- immutable attributes
vision
metabolism
sex
maximum age
- mutable attributes
wealth
location
Sugarscape as a Time-Homogeneous Markov Chain
Sugarscape “induces” a THMC:
state of the system as a 50×50 array
each array element corresponds to one patch
patch state now becomes
the patch's sugar level
whether the patch is occupied
occupying agent's state (e.g., vision, metabolic rate, wealth and life expectancy)
the number of possible states is finite since all the state variables can only take a finite set of values.
the state implies a probability distribution over the state space for the following time-step
Analysis
- irreducible THMC:
it is possible to go from any state i to any other state j in finite time
Izquierdo, Izquierdo, Galán and Santos (2009)
“the state space of the induced THMC described in the previous section is irreducible and aperiodic (also called ergodic)”
IIGS (2009)
Regenerating States
- regenerating states:
states where agents stay stationary and no sugar is collected.
Example:
every agent has vision v = 1
all agents are placed on interior desert patch
Agents do not move because the only unoccupied patches they can see have no sugar, and no sugar is collected for the same reason.
A regenerating state can produce a regenerating state: place any newborn in one of dessert patches.
Pristine State
If a regenerating state is produced four times in a row (AE's maximum sugar capacity is 4), the environment returns to its initial state: each patch's sugar level is equal to its capacity
IIGS define any such state to be a “pristine state” each patch's sugar level is equal to its capacity.
define exterminating pristine states: pristine states where
every agent dies (because every agent's sugar wealth w is no greater than its metabolic rate m).
Possible States
A state is possible if we can indentify a sequence of events that can lead to it, each with strictly positive probability.
- THMC is irreducible
i.e. it is possible to go from any state i to any state j in a finite number of time-steps.
THMC is irreducible (proof)
The proof rests on the following facts:
Let us call initial states those states that can be generated at the begginning of the simulation.
Given our definition of the state space, any state j can be reached by running the model from some initial state j0.
Any initial state j0 is reachable from any exterminating pristine state in one time-step.
To achieve this (departing from the exterminating pristine state) one only has to create the population of newborns as in state j0.
Any state i can lead to an exterminating pristine state, i.e. for every state i there exists an exterminating state ext-prist-st such that p(ni)i,ext-prist-st > 0 for some ni.
Note that one can reach a regenerating state from any state i by giving every newborn vision v = 1 and placing it in any of the patches coloured in red in figure 2.
(Note that sooner or later every agent must die because the maximum age max-age is 100.)
Reaching an exterminating pristine state from a regenerating state is straightforward: one only has to organise a synchronised genocide by "growing" agents with the desired life span –something that can be done by appropriately setting the newborns' metabolic rate m and initial wealth w0 (and vision v = 1).
A newborn with vision v = 1, metabolic rate m and initial wealth w0 placed on one of the patches painted in red in figure 2 will live Ceiling[w0/m] time-steps.
Since this procedure allows us to "grow" agents with life spans whose greatest common divisor is 1, it is possible (Bézout's identity) to organise a synchronised genocide from any regenerating state.
Having proved that the THMC is irreducible, it only remains to prove that it is also aperiodic.
To prove this it suffices to find an aperiodic state –as indicated in section 8 of our paper, after definition 7–.
Note that any exterminating pristine state ext-prist-st is clearly aperiodic, since the greatest common divisor of the set of integers n such that p(n)ext-prist-st,ext-prist-st > 0 is 1, as explained in the third bullet point of the previous list.
This concludes the proof that the induced THMC is irreducible and aperiodic, i.e. ergodic.
Ergodic THMC
In ergodic THMCs, the LR probability of finding the system in each of its states in the long run is
strictly positive
independent of the initial conditions
and the limiting distribution π coincides with the occupancy distribution π* (the long-run fraction of time that the system spends in each state).
Hence, the limiting distribution of any statistic (e.g. the sugar wealth distribution) coincides with its occupancy distribution too, and does not depend on the initial conditions.
Thus, we could approximate the limiting distribution of emergent wealth distributions in Sugarscape as much as we like by running just one simulation (with any initial conditions) for long enough.
Sugarscape Exploration, Resources, and References
Exploration
Vary the size and color of agents in order to communicate the value of two attributes, say wealth and vision.
Give each patch a
crossNeighborsattribute, which holds a mapping from each possible vision radius to a list of the neighboring locations. Determine how much faster the simulation runs when you to rely on this attribute instead of constantly recomputing the neighbors.
Resources
The original presentation of the Sugarscape model in [Epstein.Axtell-1996-MIT] is engaging and accessible. Chapter 2 includes an image of their sugarscape terrain. [Izquierdo.etal-2009-JASSS] (available on the internet) present a reproduction of this original sugarscape image.
A search engine can turn up many Sugarscape implementations in many different programming languages and simulation toolkits. Of particular interest are the following: the NetLogo implementations in the NetLogo Models library, the Mathematica implementation in chapter 14 of [Kendrick.Mercado.Amman-2006-PrincetonUP], and the very complete Python implementation in [KremerHerman.Gupta-2024_GuisadoLizar.etal]. In a somewhat technical paper, [Kehoe-2016-arXiv] works toward exact replicability by providing a formal specification of Sugarscape model.
The original presentation of the Sugarscape model in [Epstein.Axtell-1996-MIT] includes many extensions beyond the model discussed in this lecture. A web search can find video presentations of some of these on the internet. The subsequent Sugarscape literature developed many variations. For example, an early extension explores norm formation through cultural diffusion [Flentge.Polani.Uthmann-2001-JASSS]. Another extension explores the emergence of communication and cooperation in artificial societies [Buzing.Eiben.Schut-2005-JASSS].
References
Buzing, P., A. Eiben, and M. Schut. (2005) Emerging Communication and Cooperation in Evolving Agent Societies. Journal of Artificial Societies and Social Simulation 8, Article 2. http://jasss.soc.surrey.ac.uk/8/1/2.html
Epstein, Joshua M. (1999) Agent-Based Computational Models and Generative Social Science. Complexity 4, 41--60.
Epstein, Joshua M., and Robert L. Axtell. (1996) Growing Artificial Societies: Social Science from the Bottom Up. Washington, DC and Cambridge, MA: Brookings Institution Press and MIT Press.
Flentge, F., D. Polani, and T. Uthmann. (2001) Modelling the Emergence of Possession Norms Using Memes. Journal of Artificial Societies and Social Simulation 4, Article 3. http://jasss.soc.surrey.ac.uk/4/4/3.html
Izquierdo, Luis R., and Segismundo S. Izquierdo. (2009) Techniques to Understand Computer Simulations: Markov Chain Analysis. Journal of Artificial Societies and Social Simulation 12, 6. http://jasss.soc.surrey.ac.uk/12/1/6.html
Kehoe, Joseph. (2016) The Specification of Sugarscape. https://arxiv.org/abs/1505.06012
Kendrick, David A., P. Ruben Mercado, and Hans M. Amman. (2006) Computational Economics. : Princeton University Press. http://www.jstor.org/stable/j.ctvcm4g94
Kremer-Herman, Nathaniel, and Ankur Gupta. (2024) "Replacing Sugarscape: A Comprehensive, Expansive, and Transparent Reimplementation". In Guisado-Lizar, Jose-Luis and Riscos-Nu~nez, Agustin and Moron-Fernandez, Maria-Jose and Wainer, Gabriel (Eds.) Simulation Tools and Techniques, Cham: Springer Nature Switzerland.
Wilensky, Uri. (2017) NetLogo 6.01 User Manual.
Appendix: Sugarscape (Details and Hints)
Mathematica Hints for Sugarscape
Copyright © 2016–2024 Alan G. Isaac. All rights reserved.
- version:
2024-06-24